CodingTest/Algorithm
[Java / 알고리즘] 그래프 알고리즘 BFS와 DFS
마볼링
2023. 11. 27. 13:03
대표적인 그래프 탐색 알고리즘으로는
너비 우선 탐색(BFS, Breadth First Search)과 깊이 우선 탐색(DFS, Depth First Search)가 있다.
1. 너비 우선 탐색 (BFS, Breadth First Search)

- 정점들과 같은 레벨에 있는 노드들(형제 노드들)을 먼저 탐색하는 방식이다
- 위 그림에서는, A - B - C - D - G - H - I - E - F - J 순으로 탐색한다
- BFS는 재귀적으로 동작하지 않고 방문한 노드들을 차례로 저장한 후 꺼낼 수 있는 큐(Queue)를 사용한다
- 즉, 선입선출(FIFO) 원칙을 탐색한다
- 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하기 때문에 두 노드 사이의 최단 경로를 찾을 때 주로 사용한다
[코드]
import java.util.*;
public class main {
static class Graph {
Map<Character, List<Character>> adjacencyList = new HashMap<>();
void addEdge(char vertex, List<Character> neighbors) {
adjacencyList.put(vertex, neighbors);
}
void bfs(char startVertex) {
List<Character> visited = new ArrayList<>(); // 방문한 vertex 저장
Queue<Character> queue = new LinkedList<>(); // 방문할 vertex 저장, FIFO로 출력되야되기 때문에 Queue
//초기값
visited.add(startVertex);
queue.offer(startVertex);
while (!queue.isEmpty()) { // queue가 비어있지 않을때까지 반복
char currentVertex = queue.poll(); // 하나 꺼냄
// 꺼낸 currentVertex에서 인접 노드들을 꺼내 반복문
for (char neighbor : adjacencyList.getOrDefault(currentVertex, Collections.emptyList())) {
if(!visited.contains(neighbor)) { // visited에 없다면, visited와 queue에 저장
visited.add(neighbor);
queue.offer(neighbor);
System.out.println("Visited: " + visited);
}
}
}
}
}
public static void main(String[] args) {
Graph graph = new Graph();
graph.addEdge('A', Arrays.asList('B', 'C'));
graph.addEdge('B', Arrays.asList('A', 'D'));
graph.addEdge('C', Arrays.asList('A', 'G', 'H', 'I'));
graph.addEdge('D', Arrays.asList('B', 'E', 'F'));
graph.addEdge('E', Collections.singletonList('D'));
graph.addEdge('F', Collections.singletonList('D'));
graph.addEdge('G', Collections.singletonList('C'));
graph.addEdge('H', Collections.singletonList('C'));
graph.addEdge('I', Arrays.asList('C', 'J'));
graph.addEdge('J', Collections.singletonList('I'));
System.out.println("BFS starting from vertex 'A':");
graph.bfs('A');
}
}
[결과]
BFS starting from vertex 'A':
Visited: [A, B]
Visited: [A, B, C]
Visited: [A, B, C, D]
Visited: [A, B, C, D, G]
Visited: [A, B, C, D, G, H]
Visited: [A, B, C, D, G, H, I]
Visited: [A, B, C, D, G, H, I, E]
Visited: [A, B, C, D, G, H, I, E, F]
Visited: [A, B, C, D, G, H, I, E, F, J]
2. 깊이 우선 탐색 (DFS, Depth First Search)
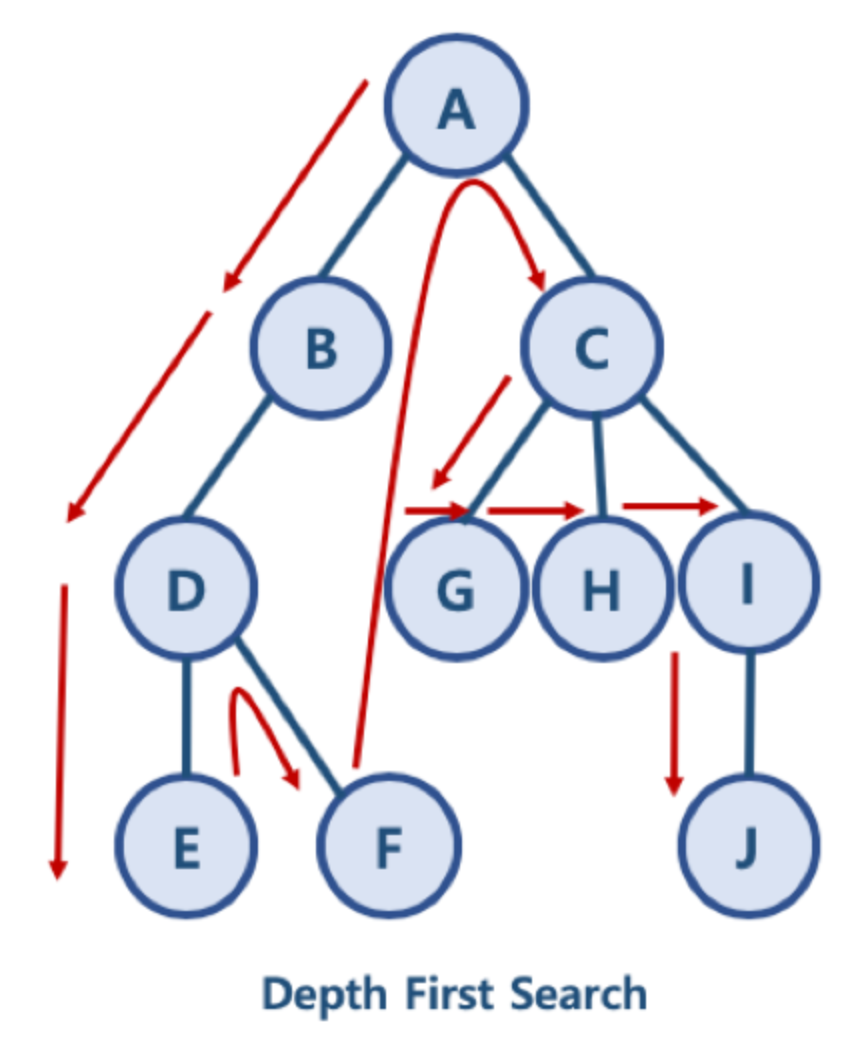
- 정점의 자식들을 먼저 탐색하는 방싱이다
- 위 그림에서는, A - B - D - E - F - C - G - H - I - J 순으로 탐색한다
- 스택(Stack)을 사용하며 LIFO원칙으로 탐색한다
- 더 이상 갈곳이 없으면 백 트랙킹(BackTracking)을 해서 돌아간다
- 주 예시 : 미로
[코드]
import java.util.*;
public class Main {
static class Graph {
Map<Character, List<Character>> adjacencyList = new HashMap<>();
void addEdge(char vertex, List<Character> neighbors) {
adjacencyList.put(vertex, neighbors);
}
void dfs(char startVertex) {
List<Character> visited = new ArrayList<>(); // 방문한 vertex 저장
Stack<Character> stack = new Stack<>(); // 방문할 vertex 저장, LIFO로 출력되야되기 때문에 Stack
// 초기값
stack.push(startVertex);
while (!stack.isEmpty()) { // stack이 비어있지 않을때까지 반복
char currentVertex = stack.pop(); // 하나 꺼냄
if (!visited.contains(currentVertex)) {
visited.add(currentVertex);
System.out.println("DFS Visited: " + visited);
}
// 꺼낸 currentVertex에서 인접 노드들을 꺼내 반복문
for (char neighbor : adjacencyList.getOrDefault(currentVertex, Collections.emptyList())) {
if (!visited.contains(neighbor)) { // visited에 없다면, visited와 stack에 저장
stack.push(neighbor);
}
}
}
}
}
public static void main(String[] args) {
Graph graph = new Graph();
graph.addEdge('A', Arrays.asList('B', 'C'));
graph.addEdge('B', Arrays.asList('A', 'D'));
graph.addEdge('C', Arrays.asList('A', 'G', 'H', 'I'));
graph.addEdge('D', Arrays.asList('B', 'E', 'F'));
graph.addEdge('E', Collections.singletonList('D'));
graph.addEdge('F', Collections.singletonList('D'));
graph.addEdge('G', Collections.singletonList('C'));
graph.addEdge('H', Collections.singletonList('C'));
graph.addEdge('I', Arrays.asList('C', 'J'));
graph.addEdge('J', Collections.singletonList('I'));
System.out.println("DFS starting from vertex 'A':");
graph.dfs('A');
}
}
[결과]
DFS starting from vertex 'A':
DFS Visited: [A]
DFS Visited: [A, C]
DFS Visited: [A, C, I]
DFS Visited: [A, C, I, J]
DFS Visited: [A, C, I, J, H]
DFS Visited: [A, C, I, J, H, G]
DFS Visited: [A, C, I, J, H, G, B]
DFS Visited: [A, C, I, J, H, G, B, D]
DFS Visited: [A, C, I, J, H, G, B, D, F]
DFS Visited: [A, C, I, J, H, G, B, D, F, E]